In previous articles, we started discussing what learning is about and techniques to learn more efficiently. But is learning always a good thing? And in particular, can we learn incorrectly? There are so many aspects to these questions that I decided to focus on only one in this article: misconceptions. I was very much looking forward to writing this article, because it’s a topic that strongly influenced my perspective on my own learning, so I hope you will like it!

First, maybe you don’t see how these questions are even interesting. When I launched the topic on Instagram, a friend came to me: “Hmm, that's a weird question! Isn’t learning always a good thing?”. I thought so. But have you never heard someone (usually a bald martial art master with a long beard) say “if you want to learn this, you need to unlearn everything you have learnt before”? Or, yourself, have you never wanted to unlearn something that has been taught to you, through bad parenting or hurtful life lessons?

Yoda knows his sh*t

To understand how this works, let’s follow the story of Josette. Just like any other person in an unquarantined reality, Josette goes around the world, lives some experiences, and learns from them.

Josette playing badminton

Today, Josette is playing badminton for the first time. She is trying to throw the birdie. She tries different ways of kicking it, and observes the effect on the resulting trajectory. For example, “if I kick softly like this, the birdie lands here, but if I kick it strongly like that, it lands over there”. To visualise this, I will use the following metaphor: Josette actions will be called input, and the effects of her actions will be called output. This way, we can visualise things with graphs, but don’t forget that this is just a metaphor. We can only push it up to a certain point.

So, we were saying: every time Josette tries something, she remembers its effect (black crosses on the following figure).

Josette observes different trajectories for different kicking techniques

Josette could learn how to play badminton by trying all the possible techniques to kick that birdie and remember their effects. But the world is too complex to remember everything by heart, and it’s also a very inefficient way to learn anything. What Josette wants to do instead, is to find a general rule that would help her predict the outcome of a new technique before trying it, so she knows if it is worth it or not. We call such a rule a model. When building such a rule (in purple on the following figures), Josette has two things in mind: first, the rule needs to explain her observations (that is go very close to all the black crosses), and it should be as simple as possible because there’s no point in overcomplicating things.

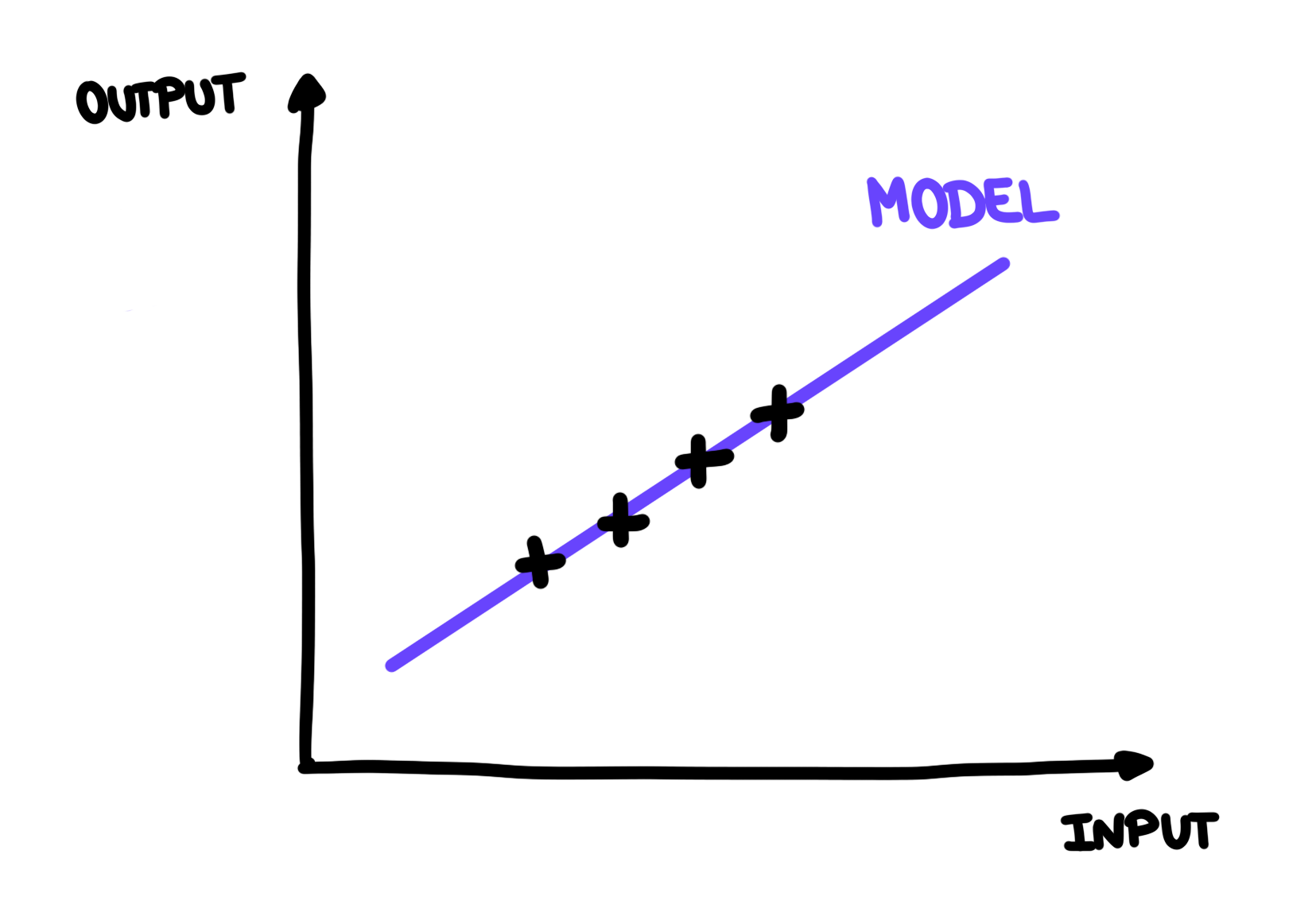
A model helps predict the outcome of an action

With this model, Josette can predict the outcome of her actions. But Josette can also figure out from the result she wants to achieve, the action she should perform. This way, she can adapt to situations very fast, even if she never encountered them before!

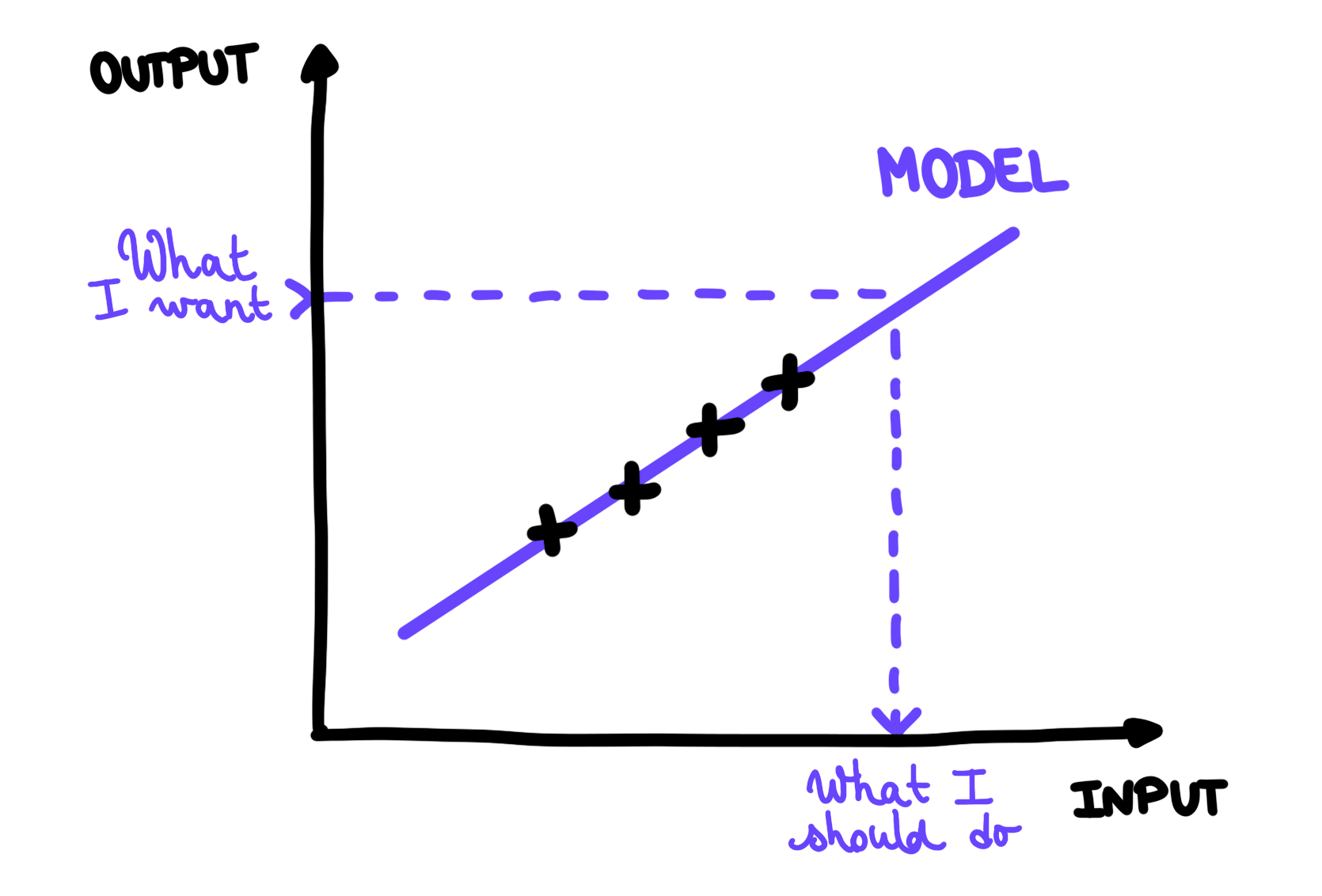
Josette uses her model to find what she should do to achieve a specific result

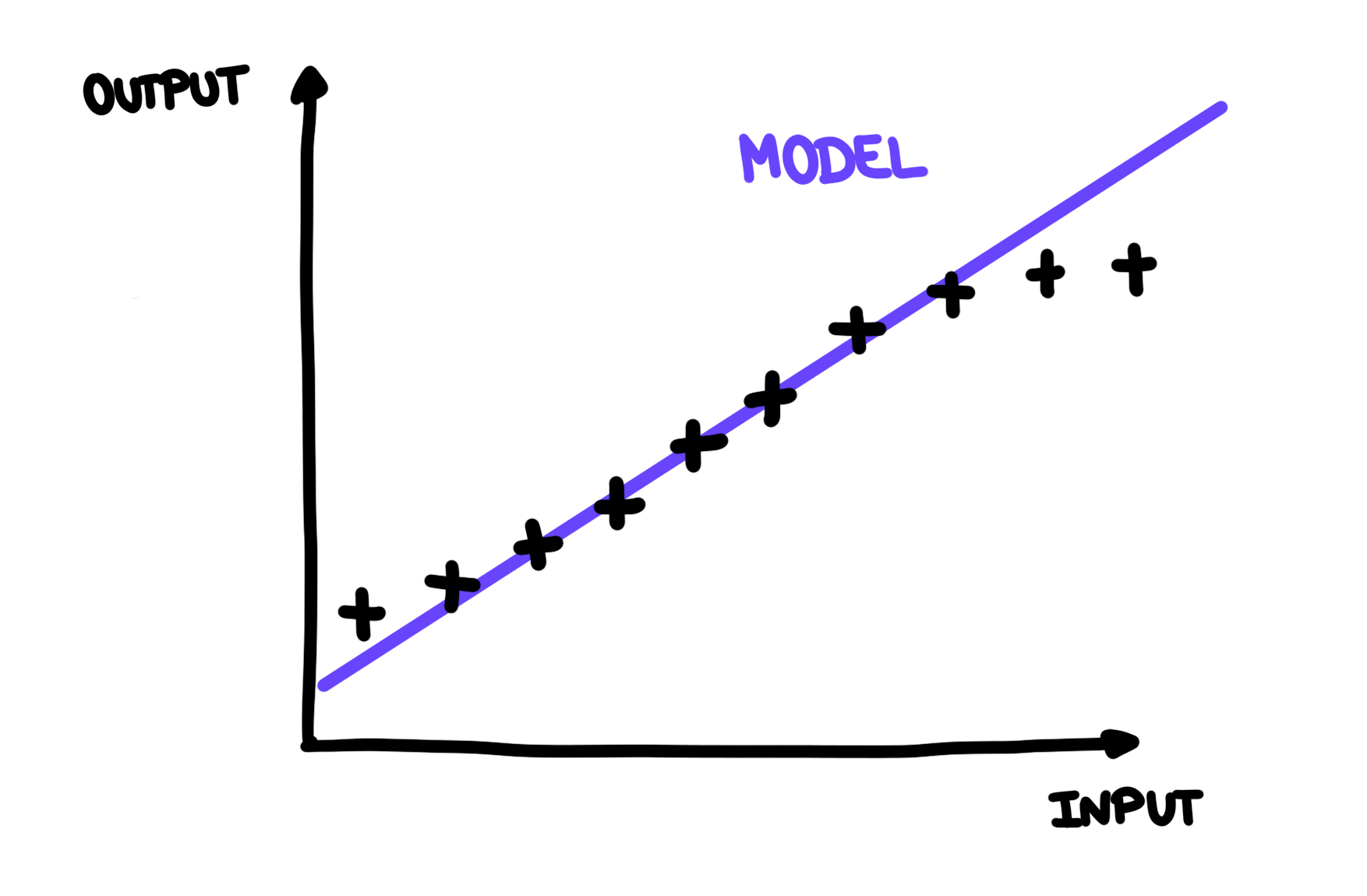
This seems great. Now what could go wrong? Many things! The first is that we build a model that is not a good generalisation of our observations and thus makes wrong predictions. For example, in the following figure, you can see that the model explains all the observation points, but doesn’t really seem trustworthy when it comes to prediction. It doesn’t seem to be the simplest explanation for our observations. Of course, maybe we could discover that, as we make more observations, this model is actually a good representation of reality, but it is very unlikely.

This model seems bad for prediction

Another problem can be that our observations don’t cover the whole picture in a meaningful way. For example, if Josette learnt how to play badminton indoors, the first time she goes outdoors with a bit of wind, a lot of her predictions will be wrong!

We have a limited field of view, our observations don’t always capture the whole picture.
Image by SMBC Comics.

So let’s add the bigger picture on our graph.

Old model on the bigger picture

As you can see, our old model doesn’t represent the bigger picture very well. If Josette had access to the bigger picture before building her model, she would have probably picked something like this:

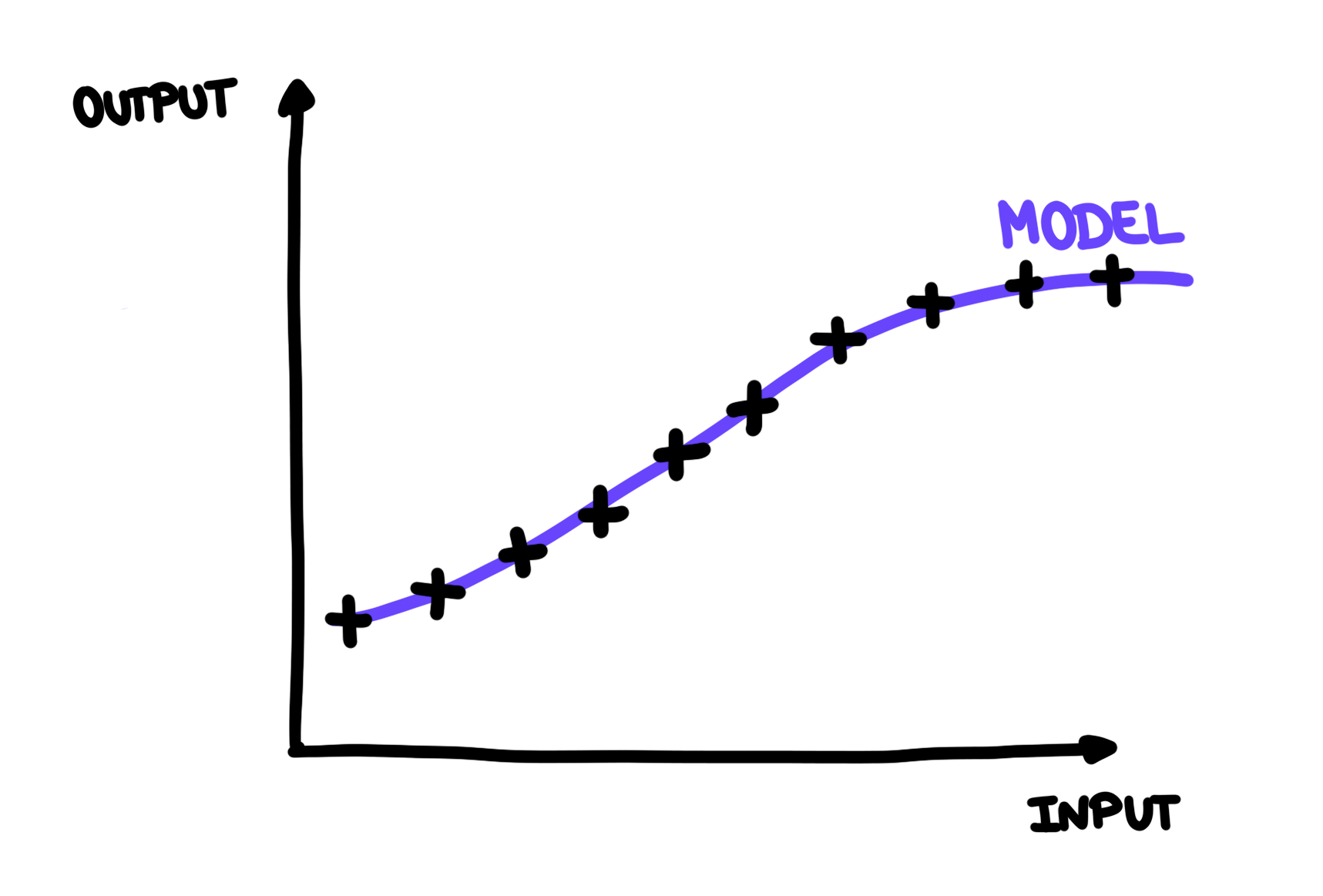
New model on the bigger picture

This is called a misconception. Formally, a misconception is “a student conception that conflicts with expert concept” [Smith III 1994]. An example of misconception that I like is from mathematics (again.) When children learn how to compare integers, they usually build an internal rule that says “if one number has more digits than another one, then it’s greater”. For example, 16,345 is greater than 14. But then, when they start learning about decimal numbers, they keep the same rule in mind. So they would conclude that 1.6345 is greater than 1.4 because it has more digits. And the problem is, that in this case, it’s actually true, even though it has nothing to do with the number of digits. The rule doesn’t generalise.

Why are misconceptions annoying? The short story is: because they are difficult to unlearn. The brain tends to stick to its old models and gets all dramatic when the outside world tries to replace them.

the extra bit_

The long story is that the world is complex, too complex for us. So our brain is building models all over the place to make sure that we can go around doing our business without being constantly overwhelmed. A strong motivation for such behaviour, is that we want to be able to predict if an action is going to give us pleasure or cause us pain, and we need to do this quickly. We are predicting machines. For example, having a model “Fire + Hand -> Pain” can prove quite useful, even if we don’t understand exactly why the flame has the effect of burning us, even if we have never seen such a flame before.

Now let’s say we learned a “wrong” model. In order to learn the “good” one, we need to give it space by removing the old one. This is very terrifying to the brain for two main reasons. First, by removing the old model, the brain is stripped off its capabilities of prediction for a while, and that makes it very anxious: what if a situation occurs, and it’s not able to protect us from danger? Second, our brain might jump to conclusions: instead of understanding that it didn’t have enough information to build a correct model, our brain might believe that its model-building skills are flawed. And this would mean that possibly all our other models are wrong. So basically, we are just going around the world, being wrong about everything, and incorrectly understanding whatever we perceive. This doesn’t seem extremely safe.

One last thing: building a model is very expensive. And storing a more complex model is also expensive. So, if our model works well enough in most of the situations that we actually encounter, why bother? For example, if Josette only plays outside once a year, why would she want to get rid of her old model that works perfectly well indoors? It’s not worth her energy.

Josette is not very seduced by this cumbersome new model

the extra bit_over_

It’s very difficult to discover on our own the misconceptions we hold, but give it a thought. Do you think you ever had to unlearn or modify a mental model as it proved inaccurate? I think I experienced this when I started to get interested in something else than mathematics. I was expecting everything to work exactly like math, and I used to be very annoyed when it didn’t. So annoyed that it prevented me from even understanding what I was trying to learn.

All in all, being aware of this tendency my brain has to protect misconceptions is really helping me out. Now, when I see that my brain starts panicking in front of new information, I can take a step back and wonder “Oh ok, this model pulled the trigger, now let’s look at it calmly. Does this model really make sense? Why am I trying to protect it so hard?”. This helps me be more patient with myself, and be more understanding with others. Again, we are all in progress, our understanding of the world is always evolving, and there’s no shortcut.

xoxo,

The Diverter

To go further:

Alan Watts - The Wisdom of Insecurity: A Message for an Age of Anxiety

I’m not on board with everything in this book, but I really appreciated the part about how important prediction is to us. The book is quite short, so I believe it’s worth the shot.

References:

[Smith III 1994] Smith III, J.P., Disessa, A.A. and Roschelle, J., 1994. Misconceptions reconceived: A constructivist analysis of knowledge in transition. The journal of the learning sciences, 3(2), pp.115-163.