Lorsque j’étais au lycée, une amie m’a dit qu’elle n’aimait pas les mathématiques parce qu’elle trouvait cela trop abstrait. Je me suis sentie assez confuse sur le moment, et je me suis dit «Mais j’aime les mathématiques parce que c’est abstrait». Cela m’a rendue curieuse: est ce que notre différence tenait vraiment au fait qu’elle n’aimait pas l’abstraction, alors que je l’appréciais ? Ou pensions-nous à des choses différentes quand nous parlions d’abstraction ? Plus concrètement : que voulons-nous dire quand nous qualifions quelque chose d’abstrait ? Que voulons-nous exactement quand nous réclamons quelque chose de plus concret ? Ces questions sont importantes, surtout dans l'apprentissage des mathématiques, parce que le pouvoir intrinsèque des mathématiques réside dans l’abstraction. Alors si l’idée d’abstraction vous rend grincheux.se, j’espère que cet article vous aidera à comprendre pourquoi certaines personnes la trouvent au contraire passionnante et enthousiasmante. Et si vous vivez pour l’abstraction, j’espère que vous trouverez quelques ici quelques perspectives nouvelles et pertinentes.

Choquée

Ces derniers mois, j’ai rassemblé des définitions de «concret» et «abstrait». En me penchant sur seulement deux articles à propos du caractère concret dans l’apprentissage des mathématiques [Fyfe 2014, Pouw 2014] j’ai par exemple découvert que le mot «concret» est associé à : significatif, familier, clair, physique, fondé, imagé, perceptible, enactif, réel, spécifique au contexte, et informel. À l’opposé, le mot «abstrait» est connecté à : général, structurel, portable, symbolique, vague, schématique. Ces exemples sont parlants : plusieurs de ces mots ne partagent absolument pas le même sens. Dire que quelque chose est vague ou n’est pas familier n'équivaut pas vraiment à dire qu’il est structurel et portable. De la même façon, l’art abstrait est très lié à nos capacités perceptives – classées comme concrètes –.

Oeuvre de l’artiste Maja Malmcrona

Pour aller plus loin, j’ai demandé à plusieurs expert.e.s manipulant l’abstraction comment ils et elles la définissent. Regardons comment ces personnes la perçoivent, et pourquoi elles sont si intriguées par cette abstraction.

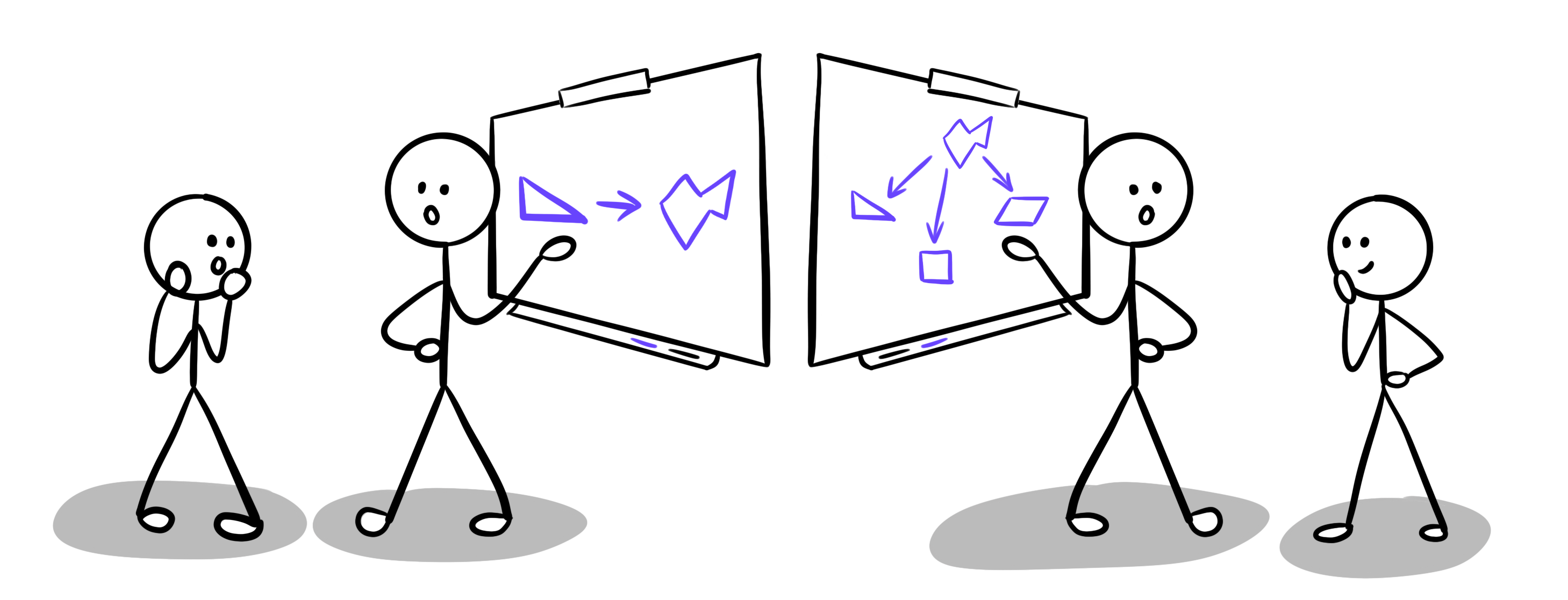
Les maths étant le point de départ de ma quête, j’ai commencé par poser la question à Vera, une collègues mathématicienne, pour voir si nous partagions une vision commune. Vera m’a répondu de cette façon : «L’abstraction signifie ’’se déplacer vers un niveau supérieur». Si on imagine les objets classés hiérarchiquement en fonction de leurs propriétés dans un arbre (de la même façon que les espèces sont classées en biologie), alors l’abstraction veut dire que vous dé-zoomez pour voir la catégorie à laquelle un objet appartient.

Définition d’une mathématicienne

Selon Vera, l'abstraction consiste à considérer une certaine situation à partir d'une perspective plus élevée dans l'arbre hiérarchique des objets mathématiques. Et c’est extrêmement puissant. Par exemple, dans l’image ci-dessus, l’arbre montre que les triangles et les quadrilatères sont des polygones, et que les polygones sont des formes. Si nous parvenons à prouver la validité d’une propriété à un niveau élevé de cet arbre, disons le niveau polygone, cela signifie que la propriété sera validée pour toutes les formes sous ce niveau. Par exemple, nous pouvons prouver que la somme des angles internes d’un polygone est égale à (nombre de côtés – 2) * 180 degrés. Cela signifie que cette formule sera valide pour tous les triangles, tous les carrés, tous les dodécagones et compagnie. Si nous n’avions pas observé les choses à partir de cette perspective globale, nous aurions dû résoudre ce problème pour chaque forme une par une : un travail plutôt fastidieux. Cela définit l’abstraction comme générale. Et cela nous mène à la prochaine définition, qui vient du mathématicien et philosophe Zmaj : «L'abstraction consiste à développer la capacité de dire, dans différents contextes, 'oh, c'est la même chose' et d'utiliser réellement cette similitude d'une manière productive.»

Définition d’un mathématicien philosophe

Une fois encore, cette définition est liée à l'idée de trouver quelque chose de similaire, quelque chose de commun à différentes situations ou différents éléments. Cependant, cette définition se concentre davantage sur les liens entre ces éléments, plutôt que sur leur catégorie. En outre, ce qui est très intéressant dans cette définition, c'est l'exigence explicite de pouvoir utiliser cette compréhension. Il ne suffit pas de remarquer que votre mur est un grand rectangle si vous ne pouvez pas appliquer ce que vous savez des rectangles pour évaluer la quantité de peinture dont vous avez besoin pour couvrir toute la surface. Cette définition considère l'abstraction comme portable.

> the extra bit_

Les informaticiens passent également beaucoup de temps à jouer avec l'abstraction. [Drew Hess] (https://twitter.com/dhess) résume l'abstraction comme "l'art de se concentrer uniquement sur les détails qui sont pertinents pour un problème/concept/objet/etc. et d'oublier tous les autres". Je pense que c'est une approche importante à considérer, car il ne s'agit pas tant de construire une abstraction explicite. Il s'agit de simplifier le problème en supprimant tous les éléments perturbateurs. Par exemple, pour en revenir à notre métaphore de la peinture murale, vous devriez vous demander quelles sont les caractéristiques du mur qui importent vraiment lorsque vous décidez de la quantité de peinture à acheter : est-ce la hauteur du mur ? sa texture ? sa longueur ? son épaisseur ? son orientation par rapport au soleil ? le nombre de tableaux qui y sont accrochés ? Drew conclut en disant que "l'objectif est de rendre la solution/description aussi générale que possible tout en restant efficace pour résoudre le problème ou identifier le sujet."

Définition d’un informaticien

Bladyjoker affirme que l'abstraction est très importante pour la programmation. Il explique notamment que "les programmeurs identifient les similitudes et les différences de code, ce qui leur permet de formuler une forme de code plus générale qui est utilisée pour exprimer les formes spécifiques." Concrètement, les programmeurs veulent pouvoir réutiliser le code autant que possible, afin de le compresser et de le rendre plus facile à maintenir. Bladyjoker explique que certains langages, comme Haskell, permettent de voir et d'extraire facilement ces composants réutilisables, tandis que d'autres, comme Java, rendent la tâche un peu plus fastidieuse. Mais Bladyjoker nous invite à faire attention lors de l'abstraction : si l'abstraction devient trop générale, les gens pourraient ne plus pouvoir s'y connecter et finir par ne plus utiliser la fonctionnalité.

Définition d’un programmeur

> the extra bit_over_

Allons maintenant un peu plus loin et examinons la linguistique, c'est-à-dire l'étude des langues. KC, notre expert sous couverture, explique que "l'abstraction est le processus qui consiste à extraire d'un ensemble diversifié de choses un modèle commun et général". N'est-ce pas merveilleux que "abs-tract-ion" et "ex-tract-ion" aient une racine commune ? Il est intéressant de noter qu'en arabe, "tajriid" (abstraction) vient de la racine "jarada", qui signifie enlever, dépouiller.

Définition d’un linguiste

Cette définition englobe très bien l'idée d'abstraction formulée par notre première mathématicienne, Vera. Nous abstrayons en extrayant l'essentiel d'une famille d'objets. En outre, la définition de KC insiste également sur l'aspect suppression des détails superficiels pour atteindre l'essence d'un objet.

En parlant maintenant d'essence, que disent les artistes de l'abstraction ? [Maja Malmcrona] (https://www.majamalmcrona.com/) affirme que "dans l'art, abstraire signifie dévoiler. C'est une tentative de découvrir l'essence d'une expérience en mettant au jour ses propriétés les plus fondamentales par la suppression des éléments extérieurs superficiels." Ces propos sont très proches de ce que nous avons vu en étudiant la science. Mais qu'est-ce que cela signifie pour l'art ? Qu'est-ce que l'essence d'une expérience ? Maja explique que "l'art abstrait ne cherche pas à représenter la réalité telle que nous la voyons, mais plutôt à communiquer la réalité telle que nous la sentons. Il ne s'inspire pas de notre réalité extérieure d'objets et de figures, mais de notre réalité intérieure de concepts et d'émotions. Elle préfère les sensations au visuel, les universaux aux particuliers". Et c'est en cela que nous comprenons le processus de l'art abstrait. D'abord, il y a l'honnêteté et l'introspection, qui vous font regarder directement les changements que certaines situations créent en vous. Ensuite, il y a le courage d’en faire quelque chose et de le montrer et l’exposer au monde.

Définition d’une artiste

Je pense qu'il y a une certaine ironie à dépeindre nos modèles internes dans le monde extérieur, par le biais de supports physiques et, pourrait-on dire, concrets. Et, quand on y pense, cette ironie se retrouve dans tous les domaines que nous avons explorés plus tôt dans cet article. N'est-il pas intéressant de voir comment les mathématiciens ont dû construire un tout nouveau langage constitué de symboles afin de pouvoir communiquer leur compréhension du monde ? Et en mathématiques comme en art, plus vous commencez à comprendre le langage ainsi que vos propres représentations internes, plus l'abstrait devient identifiable.

Art abstrait et maths abstraites [1]

Pour conclure notre quête, j'ai demandé à une philosophe, que nous appellerons Ieva, de me faire part de ses réflexions sur l'abstraction. Sa réponse était très complète et intéressante [2]. Un commentaire que j'ai trouvé important à méditer est le fait que "'abstraire' peut aussi être connoté négativement, pour signifier que quelque chose est indûment retiré de l'idée plus complexe." S'il n'est pas nécessaire d'extraire quelque chose de son contexte, s'il n'est pas nécessaire de réutiliser une compréhension sous-jacente ailleurs, pourquoi s'embêter avec l'abstraction ? Ieva a également soulevé l'idée intéressante que certaines choses pourraient être inhérentes à l'abstraction. La plupart des définitions que nous avons vues jusqu'à présent se concentrent sur cette idée de l'abstraction comme partant du concret, et obtenue par l'identification de modèles communs, la suppression de détails superficiels, ou la formation de connexions. Mais peut-on définir l'abstraction sans instances concrètes ? Dans ce cas, elle affirme que "l'une des solutions consiste à créer une "concrétude" artificielle, par exemple à l'aide de technologies éducatives qui nous permettent d’expérimenter des choses que nous ne pouvons généralement pas appréhender avec nos propres sens. Par exemple, nous pouvons créer des animations 3D de processus chimiques que nous ne pourrions pas voir de nos propres yeux." Ici, c'est l'inverse qui se produit. Comme nous l'avons vu avec l'art, nous essayons de concrétiser quelque chose d'abstrait. Ce qui nous laisse avec une question : "Y a-t-il quelque chose de perdu dans le processus de 'désabstraction' ?"

Question philosophique

Dans cet article, nous avons demandé à des experts de différents domaines de nous donner leur définition de l'abstraction. Dans plusieurs domaines, comme les mathématiques et l'informatique, l'abstraction est présentée comme quelque chose de général qui peut être réutilisé de manière productive. L'abstraction est donc très utile car, avec un seul outil, nous sommes désormais en mesure de résoudre une myriade de problèmes. Afin de construire cette abstraction productive, il est important de dépouiller les instances concrètes des détails superficiels. Cette approche est évoquée par les mathématiciens, les informaticiens, les linguistes, mais aussi les artistes et les philosophes. Dans tous ces domaines, l'abstraction consiste à atteindre l'essentiel, le cadre structurel qui se cache derrière tous les objets et expériences concrets.

En somme, nous avons vu comment les experts s'accordent à dire que l'abstraction est portable, productive et essentielle. Mais pourquoi les gens utilisent-ils parfois ce mot pour décrire quelque chose de vague et de peu familier ? Comme nous l'avons remarqué, lorsqu'elle est présentée nue, l'abstraction ne ressemble pas nécessairement à ce que nous sommes susceptibles de rencontrer dans notre vie quotidienne. Même si vous êtes capable d'abstraire un modèle interne productif à partir de vos expériences concrètes, il n'est pas toujours facile d'exprimer cette compréhension dans le monde physique. Comme le montrent les mathématiques et l'art, les experts ont dû développer un langage spécifique afin de pouvoir extérioriser cette compréhension et en discuter. Si vous ne parlez pas ce langage et ne disposez pas du soutien nécessaire pour l'apprendre, vous risquez fort de passer à côté de l'essentiel et de vous sentir confus.

Lorsque l'on utilise le mot "abstrait", les gens peuvent de fait vouloir dire des choses différentes ou, plutôt, mettre l'accent sur des aspects différents de l'abstraction. Lorsque mon amie a dit que les mathématiques étaient trop abstraites pour elle, elle faisait référence à l'absence de familiarité initiale de tout cela. Et en retour, lorsque je me suis penché sur ma propre affection pour l'abstraction, j'ai constaté que j’avais dépassé le point de la non-familiarité et que je me référais plutôt à sa portabilité.

Enseigner l’abstraction

Si nous revenons à l'éducation, il y a quelques éléments importants à comprendre. Premièrement, il n'est pas toujours raisonnable d'abstraire d'emblée. Comme Ieva l'a mentionné, si l'abstraction est présentée comme étant seulement une représentation alternative de quelque chose de plus concret (et, dans ce cas, plus familier), les étudiants n'auront pas beaucoup d'incitation à se souvenir et à comprendre cette représentation étrangère, et pourraient simplement la rejeter. Cependant, si l'abstraction est présentée comme une solution à plusieurs problèmes relatifs, et qu'elle est accompagnée d'outils adaptés pour communiquer à son sujet, elle devient soudainement infiniment plus précieuse.

xoxo,

The Diverter

PS1 : Un grand merci à tous les experts qui ont contribué à l'article et aidé à la relecture !

PS2 : Les jolis dessins utilisés dans mes pas-si-jolis dessins ont été réalisés par la talentueuse Maja Malmcrona et utilisés avec sa permission. Si vous aimez l'art, la philosophie et la vie, allez lui donner un peu d'amour, parce qu'elle est incroyable ! (website) (instagram) (podcast)

Pour aller plus loin :

L’échelle de l’Abstraction par Bret Victor.

Vous pouvez également lire cet article :

Wagner, R., 2019. Mathematical Abstraction as Unstable Translation Between Concrete Presentations. Philosophy of Mathematics Education Journal, 35.

Cet excellent ouvrage décrit l'abstraction mathématique comme une traduction entre les objets (ou leurs représentations) plutôt que la construction d'une sorte de représentation idéale. L'article est fondé sur l'histoire des mathématiques et de l'enseignement des mathématiques.

Notes :

[1] Un diagramme de Voronoï dans son habitat naturel :

[2] La citation complète : Le terme "abstrait" peut être une caractéristique d'une idée ou d'une chose. En tant que caractéristique, pour moi, "abstrait" est le contraire de "concret", c'est-à-dire manifesté dans un contexte, ou empirique. Décrire une chose comme étant abstraite signifie la considérer comme étant éloignée des occurrences spécifiques, réduite à l'essence qui nous permet de reconnaître une chose comme telle. Nous faisons l'abstraction (en tant que verbe) lorsque nous essayons de reconnaître quelque chose comme quelque chose sans expérience. Le terme "abstrait" peut également être connoté négativement, pour signifier que quelque chose est indûment éloigné d'une idée plus complexe. Pour moi, il est assez intéressant de penser à quelque chose - une chose ou une idée - comme étant intrinsèquement abstrait, et non comme étant "abstrait" de quelque chose. Il semble que certaines choses, par exemple des concepts particuliers en mathématiques ou en physique, mais aussi en art, soient décrites comme intrinsèquement "abstraites". Une peinture abstraite, par exemple, n'est pas une réduction d'un dessin concret et exact d'une "chose" ; elle est abstraite et seulement abstraite. En quoi cette idée, à savoir que quelque chose est intrinsèquement abstrait, est-elle liée à l'idée de "l'abstrait" comme opposé au "concret" ? Je pense que cette différence est assez importante, surtout si nous pensons à l'apprentissage et à l'enseignement. Dans le cas de "l'abstrait", opposé au "concret", nous partons souvent du principe, d'un point de vue didactique, que nous devons passer du concret à l'abstrait : il faut d'abord essayer quelque chose, puis apprendre les idées sous-jacentes. Mais que faire si quelque chose est intrinsèquement abstrait ? Une solution consiste à créer une "concrétude" artificielle, par exemple à l'aide de technologies éducatives qui permettent de faire l'expérience de choses que nous ne pouvons pas expérimenter avec nos propres sens. Par exemple, nous pouvons créer des animations 3D de processus chimiques que nous ne pourrions pas voir de nos propres yeux. Une autre solution consiste à enseigner une chose (intrinsèquement) abstraite comme étant (intrinsèquement) abstraite. En pensant à la solution 1, je ne peux m'empêcher de me demander : Qu'est-ce que nous enseignons ? Comment peut-on enseigner quelque chose d'INHÉRENTEMENT abstrait comme étant concret ? Y a-t-il quelque chose de perdu dans le processus de "désabstraction" ?"

Références :

[Fyfe 2014] Fyfe, E.R., McNeil, N.M., Son, J.Y. and Goldstone, R.L., 2014. Concreteness fading in mathematics and science instruction: A systematic review. Educational psychology review.

[Pouw 2014] Pouw, W.T., Van Gog, T. and Paas, F., 2014. An embedded and embodied cognition review of instructional manipulatives. Educational Psychology Review.